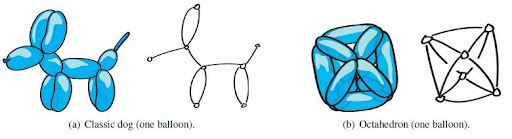
Two one-balloon constructions and their associated graphs
The interest about ballon twisting was motivated by...
Balloon twisting is fun: the activity can both entertain and engage children of all ages. Thus balloon twisting can be a vehicle for teaching mathematical concepts inherent in balloons. As we will see, these topics include graph theory, graph algorithms, Euler tours, Chinese postman tours, polyhedra (both 3D and 4D), coloring, symmetry, and even NP-completeness. Even the models alone are useful for education, e.g., in illustrating molecules in chemistry.There's also a second motivation: building architectural structures with air beams (Army blows up building, Center manages technology of inflatable composite structures).
Our approach suggests that one long, low-pressure tube enables the temporary construction of inflatable shelters, domes, and many other polyhedral structures, which can be later reconfigured into different shapes and re-used at different sites. In contrast to previous work, which designs a different inflatable shape specifically for each desired structure, we show the versatility of a single tube.
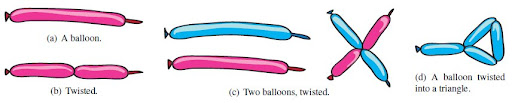
Twisting baloons
(...) a bloon is a (line) segment which can be twisted at arbitrary points to form vertices at which the bloon can be bent like a hinge. The endpoints of a bloon are also vertices. Two vertices can be tied to form permanent point connections. A twisted bloon is stable if every vertex is either tied to another vertex or held at a nonzero bending angle.The three researchers also defined two models
- (Simple) twisting: Every subsegment of a bloon between two vertices forms an edge in the associated graph, representing an inflated portion of a balloon.
- Pop twisting: Some subsegments of a bloon between two vertices can be marked as deflated, causing them not to appear in the associated graph. Such deflated segments can be achieved with physical balloons by squeezing or sucking the air down the balloon or by popping a segment between two existing vertices (a practice common in balloon twisting, though requiring some care and skill).
Th.1: A graph has bloon number $1$ if and only if the graph is Eulerianand
Th.2: A graph with $o > 0$ odd vertices has bloon number $o/2$.In the pop twisting model the main problem is to minimize the bloon's lenght. The problem is equivalent to the Chinese postman problem (Nist, MathWorld): we must find a cyclic path of minimum lenght in a undirected graph. If the graph has an eulerian circuit, that circuit is an optimal solution (Wikipedia).
In the case of the pop twisting model the following theorem is true:
Th.3: There is a polynomial-time algorithm that, given a graph and a desired $k \geq 1$, finds the $k$ bloons of minimum total length that pop-twist the graph.where $k$ is the numbers of bloon's paths.
Now, before see the applications of the theory, there's the last theorems about Hoyler's problem in bloon model. We can define the problem in these therms:
decide whether the edges of a graph can be decomposed into copies of a fixed graph $H$.In 2009 Krzysztof Bryś and Zbigniew Lonc resolved the problem, and from this starting point researchers proof the following theorem:
Th.4: Every graph with unit edge lengths can be twisted from doubloons and possibly one demidoubloon (when the graph has an odd number of edges).In this case we can define an $l$-bloon like a bloon with lenght $l$, where $l$ is integer.
Using Th.4 and the following two theorems we can mathematically proof the platinic twisting.
Th.5: It is NP-complete to decide whether a planar bipartite graph with unit edge lengths can be simply twisted from $l$-bloons.
Th.6: It is strongly NP-complete to decide whether a planar 3-connected graph with $o$ odd vertices can be simply twisted from $o/2$ equal-length bloons.I remeber that for NP-problems we intend a class of decisional problems that we can resolve in a polynomial time.
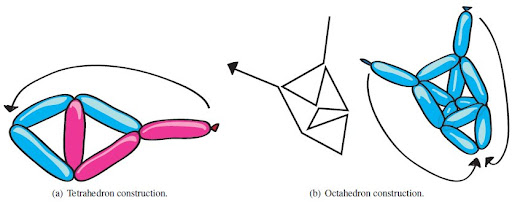
Constructing two platonic solids

Examples of one-balloon polyhedra


Platonic balloons

Five intersecting tetrahedra (fifteen balloons).
Demaine E.D., Demaine M.L. & Hart V. (2008). Computational balloon twisting: The theory of balloon polyhedra., Proceedings of the 20th Canadian Conference on Computational Geometry (CCCG2008), 139-142.
Bryś K. & Lonc Z. (2009). Polynomial cases of graph decomposition: A complete solution of Holyer's problem, Discrete Mathematics, 309 (6) 1294-1326. DOI: 10.1016/j.disc.2008.01.054
Bryś K. & Lonc Z. (2009). Polynomial cases of graph decomposition: A complete solution of Holyer's problem, Discrete Mathematics, 309 (6) 1294-1326. DOI: 10.1016/j.disc.2008.01.054

No comments:
Post a Comment
Markup Key:
- <b>bold</b> = bold
- <i>italic</i> = italic
- <a href="http://www.fieldofscience.com/">FoS</a> = FoS