Butterflies, hurricanes and... pools!

Chaos is nothing more than order seen from the opposite side.

This defintion by Fethry Duck in the italian story Il mobile caotico (The chaotic furniture) can be considered very centered on the heart of chaos. And the mathematical tool that we used to study it is the theory of chaos.

Flapping the wings

What best identifies chaos theory is the butterfly effect, which identifies in a simple and effective way the strong dependence of chaotic systems on initial conditions. The name was first used by Edward Lorentz, who published the first article on this effect in 1963⁽¹⁾.
The popular version of the butterfly effect goes something like this: The flapping of a butterfly's wings in Brazil causes a hurricane in New York and the use of the butterfly was probably suggested to Lorentz from Ray Bradbury's 1952 short story A sound of thunder in which an unwary time traveler, stepping out of the path set by the travel agency and thus stepping on a butterfly, even manages to change the result of the last US presidential elections, allowing a fascist to become the most powerful man on the planet!
From a scientific point of view, one of the most typically chaotic problems is that of weather forecasts, because of the large amount of variables that are present. The appearance of chaotic behaviors, however, would not be so scientifically interesting if it were not for one of their particular characteristics: the fundamental laws that govern, for example, time are deterministic and individually easily solved, but by combining together a large number of such equations, not only the resolution of the system is more complicated, so much so that it is necessary to use electronic calculators, but also the solution shows a chaotic behavior graphically well identified by the Lorentz attractors:

The image above shows the trend of a chaotic system. Its position is variable, even a lot, over time, but it has an interesting feature: the system oscillates around two stable points, the two attractors, for example good and bad weather, just to stay on the subject of weather forecasts, or two gravitational centers if we try to study the system of three bodies in space, such as the Sun, Earth and Moon.
Indeed the three-body problem is another typical example of a chaotic system, as emerged from the numerical resolution of the problem. Obviously the Sun-Earth-Moon does not show such ùchaotic patterns, but let's not forget that the solar system itself is much more complex than these three objects alone.
The central point of chaos theory is that, to obtain statistical behavior, it is not necessary to start from statistical laws, but it is the high number of variables that complicate the matter.

The statistical billiards

An interesting mathematical system that exhibits chaotic behavior is dynamical billiards⁽²⁾. As in real billiards, we have a table on which a ball is thrown. This, as in real billiards, will hit the edges bouncing according to the usual laws of billiards, but unlike the real one, there are no holes in which to fall or friction to slow down the motion of the ball, which will continue to move forever. Furthermore, a dynamical billiard table can also have edges with shapes different from the straight ones typical of the rectangle or even be multidimensional. What unites all these dynamical billiards is the chaotic behavior of the ball and the ergodic characteristic of its motion: the ball, in fact, sooner or later, will hit all points of the billiard's edge. This fact, however, does not make it easier to predict the behavior of the ball, on the contrary it complicates the prediction, precisely because the ball, and more generally a chaotic system, can do exactly what it likes according to the surrounding conditions.
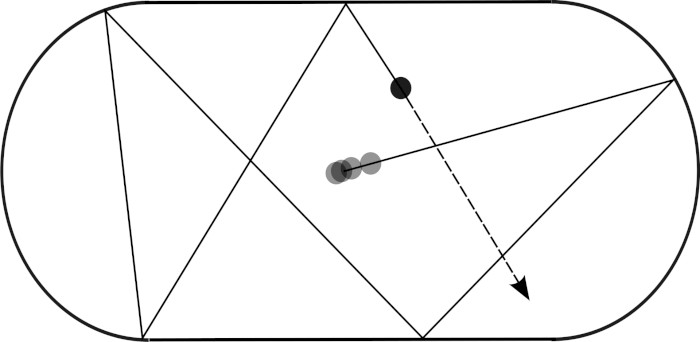
But what somehow simplifies weather predictions, making them somehow more accurate, is an interesting result known as Birkhoff's ergodic theorem, discovered in 1931 by the american mathematician George David Birkhoff. The theorem states that, although it cannot exactly predict the trajectory of a ball in a dynamic pool, it is possible to accurately predict how much time the ball will spend in a given region of the table. For example, if we are observing a gas, then even if we are not able to say exactly where its particles will be found at all times, we will still be able to predict quantities such as pressure and temperature.

Dynamical billiards, however, have not ceased to amaze mathematicians. Let's take the Ehrenfest model. Proposed in 1907 by Paul Ehrenfest and his wife Tatyana Afanasyeva to explain the second law of thermodynamics, it considers N particles in a container divided into two zones. The particles pass from one area to another independently according to a certain exchange rate. The two physicists, however, were not satisfied with this model and in 1912 proposed a variation of it, the wind-tree model⁽³⁾, that is a gas that moves inside an infinite container but with rectangular obstacles inside.
Well, in 2011 the two mathematicians Corinna Ulcigrai and Krzysztof Fraczek studied a generalized version of the model, obtaining an unexpected result⁽⁴⁾: the trajectories were not ergodic! Therefore, complicating the situation does not necessarily lead to chaotic behavior.

---

1. Lorenz, E. N., 1963, Deterministic nonperiodic flow, Journal of the atmospheric sciences, vol.20, n.2, pp. 130-141 doi:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 ↩︎
2. Leggi anche Chaos on the billiard table di Marianne Freiberger. ↩︎
3. P. and T. Ehrenfest, Begriffliche Grundlagen der statistischen Auffassung in der Mechanik Encykl. d. Math. Wissensch. IV 2 II, Heft 6, 90 S (1912). ↩︎
4. Frączek, K., & Ulcigrai, C. (2014). Non-ergodic $\mathbb {Z}$-periodic billiards and infinite translation surfaces. Inventiones mathematicae, 197(2), 241-298. doi:10.1007/s00222-013-0482-z ↩︎