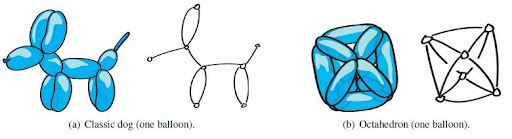
Two one-balloon constructions and their associated graphs
The interest about ballon twisting was motivated by...
Balloon twisting is fun: the activity can both entertain and engage children of all ages. Thus balloon twisting can be a vehicle for teaching mathematical concepts inherent in balloons. As we will see, these topics include graph theory, graph algorithms, Euler tours, Chinese postman tours, polyhedra (both 3D and 4D), coloring, symmetry, and even NP-completeness. Even the models alone are useful for education, e.g., in illustrating molecules in chemistry.There's also a second motivation: building architectural structures with air beams (Army blows up building, Center manages technology of inflatable composite structures).
Our approach suggests that one long, low-pressure tube enables the temporary construction of inflatable shelters, domes, and many other polyhedral structures, which can be later reconfigured into different shapes and re-used at different sites. In contrast to previous work, which designs a different inflatable shape specifically for each desired structure, we show the versatility of a single tube.
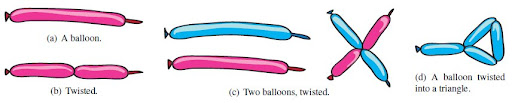
Twisting baloons
(...) a bloon is a (line) segment which can be twisted at arbitrary points to form vertices at which the bloon can be bent like a hinge. The endpoints of a bloon are also vertices. Two vertices can be tied to form permanent point connections. A twisted bloon is stable if every vertex is either tied to another vertex or held at a nonzero bending angle.The three researchers also defined two models




